728x90
강화학습이란?
- "순차적 의사결정 문제 에서 누적 보상을 최대화 하기 위해 시행착오를 통해 행동을 교정하는 학습 과정"
- 쉽게 말해, "시행착오를 통해 발전해 나가는 과정"
- 그림 1 과 같이 머신러닝의 한 부류로 비지도 및 지도 머신러닝과 다르게 정적 데이터셋에 의존하는 것이 아니라 역동적인 환경에서 동작하며 수집된 경험으로 부터 학습한다.

사진 설명을 입력하세요.
강화학습이란?
- 쉽지만 추상적인 버전
- “시행착오(train and error)를 통해 발전해 나가는 과정
- 어렵지만 좀더 명확한 버전
- “순차적 의사결정 문제에서 누적 보상을 최대화 하기 위해 시행착오를 통해 행동을 교정하는 학습과정”
순차적 의사결정 문제
- 에이전트가 시간 순서대로 행동을 선택하고 환경으로부터 피드백을 받아 학습하는 문제
- 결과에서 얻은 보상을 통해 미래의 행동을 개선함 (Markov Decision Process (MDP)) 요소가 포함

사진 설명을 입력하세요.
- 강아지 훈련의 강화학습
- 강아지를 둘러싼 환경과 조련사를 포함한 환경에서 행동을 완료하도록 강아지를 훈련하는 것
- 관측값: 조련사가 강아지에게 명령 또는 신호를 보내고 강아지는 이를 관찰
- 강아지는 행동을 취하여 응답
- 취한 행동이 원하는 행동과 근접한 경우 조련사는 간식 또는 장남감과 같은 보상 제공
- 근접하지 않은 경우 보상이 제공되지 않음
- 훈련 초반에 강아지는 특정 관측값을 행동 및 보상과 연관 짓기 위해 “앉아”라는 명령에 구르는 등 무작위 행동을 더 많이 취할 것이다.
- 이러한 관측값과 행동 사이의 연관성 또는 매핑을 정책이라함 - 강아지 관점에서 최적의 시나리오는 모든 신호에 올바르게 응답하여 최대한 많은 간식을 획득하는 것이다.
- 강화학습 훈련의 의미는 강아지가 보상을 최대화하는 목표 행동을 배울 수 있도록 강아지의 정책을 “조정”하는 데 있다.
- 훈련 완료시 강아지는 자신이 개발한 내부 정책을 사용하게 되며 보호자의 “앉아”라는 명령을 관찰하고 적절한 행동을 취할 수 있게 된다. (이 정도 시점에서는 간식이 제공되면 좋지만 필수적이지는 않다)
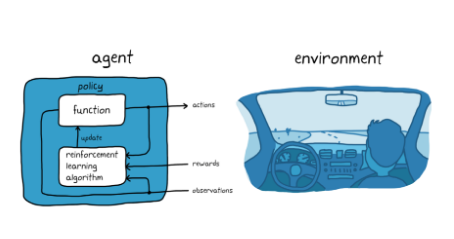
사진 설명을 입력하세요.
자율주차의 강화학습(자율주행 시스템을 사용한)
- 강화학습을 활용하여 자동차 컴퓨터(에이전트)에게 올바른 주차 위치에 주차하도록 가르치는 것 (목표)
- 환경: 에이전트를 제외한 모든 것으로 차량의 동특성, 근처의 다른 차량, 날씨
- 관측값: 에이전트는 훈련동안 카메라, GPS 및 라이다 등 센서의 판독값을 사용
- 행동 : 운전, 제동 및 가속 명령을 생성
- 정책조정: 관측값으로부터 올바른 행동을 생성하는 방법을 학습, 시행착오 절차를 통해 차량의 주차를 반복해서 시도
- 보상: 시행의 적합성을 평가하고 학습 과정을 인도하기 위해 보상 신호를 제공
게임 플레이
- 에이전트는 게임의 현재 상태(게임화면, 플레이어의 위치)에서 어떤 행동(이동, 공격, 아이템 사용)을 선택해야 하는지 결정해야한다.
- 선택한 행동에 따라 게임 상황이 변하고, 에이전트는 그 결과로 얻은 보상을 통해 미래의 행동을 개선해 나간다.
- 행동 (Action): 에이전트가 취할 수 있는 행동, 예를 들어 이동, 공격, 아이템 사용 등.
- 보상 (Reward): 각 행동에 대한 환경으로부터의 피드백. 예를 들어, 적을 공격하여 처치하면 양의 보상을 얻고, 피해를 입으면 음의 보상을 얻음.
- 정책 (Policy): 상태에 따라 에이전트가 어떤 행동을 선택할지 결정하는 전략.
- 가치 함수 (Value Function): 특정 상태 또는 상태-행동 쌍의 가치를 평가하는 함수.
강화학습 워크플로
- 강화학습을 사용한 에이전트 훈련의 일반적인 워크플로는 다음과 같은 단계를 포함
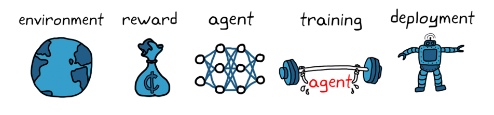
사진 설명을 입력하세요.
- 환경 생성
- 에이전트와 환경 간 인터페이스 등의 강화학습 에이전트가 운영될 환경을 정의
- 환경은 시뮬레이션 모델 또는 실제 물리적 시스템일 수 있으나 더 안전하고 실험이 가능한 시뮬레이션 환경이 일반적으로 더 좋은 첫 단계이다.
- 보상 정의
- 에이전트가 성과를 적업 목표와 비교하기 위해 사용할 보상 신호 및 이 신호를 환경으로부터 계산하는 방법을 명시해야함.
- 보상을 설정하는 것이 매우매우 까다로운 작업이고, 올바른 보상설정을 위해서는 다양한 시도가 필요함
- 에이전트 생성
- 정책과 강화학습 훈련 알고리즘으로 구성된 에이전트를 생성한다.
- 정책을 나타낼 방법 선택( 신경망 또는 룩업 테이블 사용 )
- 적절한 알고리즘의 선택 (각각의 특정 훈련 알고리즘의 범주와 연결되어 있으며, 일반적으로 대부분의 최신 강화학습 알고리즘은 대규모 상태/행동 공간 및 복잡한 문제에 적합한 신경망에 의존한다.)
- 에이전트 훈련 및 검증
- 훈련 옵션(중지 기준) 을 설정하고 에이전트를 훈련해 정책을 조정한다. 훈련이 종료된 후 훈련된 정책을 꼭 검증하여야 하며, 필요에 따라 보상 신호 및 정책 아키텍처 등의 설계 선택을 다시 검토하고 재훈련한다.
- 강화학습은 일반적으로 샘플 비효율적으로 알려져 있고, 훈련은 응용 분야에 따라 몇 분에서 며칠까지 소요된다. 복잡한 응용 분야의 경우 여러 CPU, GPU 및 컴퓨터 클러스터에서 훈련을 병렬 처리하여 가속할 수 있다.

사진 설명을 입력하세요.
- < 병렬 연산으로 샘플 비효율적인 학습 문제 훈련 >
- 정책 배포
- 정책은 독립된 의사 결정 시스템으로 강화학습을 사용하여 에이전트를 훈련하는 절차를 반복하는 과정
- 마르코프 결정 프로세스(MDP: Markov Decision Process)
- 순차적 의사결정 문제는 결국 MDP라는 개념을 통해 더 정확하게 표현이 가능하다.
- 아이가 잠이 드는 마르코프 프로세스

사진 설명을 입력하세요.
- 아이가 취할 수 있는 상태
- 누워 있는 상태 S0
- 일어나서 노는 상태 S1
- 눈을 감은 상태 S2
- 서서히 잠이 오는 상태 S3
- 잠든 상태 S4
- 하나의 상태에서 다른 상태로 전이가 일어남
- S4의 경우 종료 상태
- MP(Markov Process)
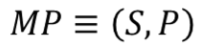
사진 설명을 입력하세요.
- 마르코프 프로세스는 상태(S)와 전이행률행렬(P)로 정의
- 마크코프 성질
- 마르코프 성질의 정의

사진 설명을 입력하세요.
- 상태(St)일때 상태(St+1)로 전이 될 확률
- 마르크프 성질의 뜻
- 미래는 오로지 현재에 의해 결정된다.
- 상태(St)가 되기까지의 과정은 확률 계산에 영향 X
- 마르코프한 상태
- 체스 게임
- 한 수 이전 혹은 그 전의 상황의 영향 X
- 어느 시점 t의 사진 한 장으로 체스의 다음수 결정 가능
- 마르코프하지 않은 상태
- 운전하고 있는 운전자의 상태
- 어느 시점 t의 사진 한 장으로 의사결정 불가능
- 앞으로 가고 있는지, 뒤로 가는지 확인 불가
- 10초 동안의 사진 10장을 묶어서 상태로 제공하면 좀 더 마르코프한 상태에 가까워짐
- 진행 방향, 속도, 가속도 등의 정보를 함께 제공하여 마르코프한 상태 만족
- 어떤 현상을 마르코프 프로세스로 모델링하려면 상태가 마르코프 해야하고, 단일 상태 정보만으로도 정보가 충분하도록 상태를 구성해야 함
마르코프 리워드 프로세스
마르코프 프로세스에 보상의 개념의 추가되면 마르코프 리워드 프로세스이다.
아이가 잠이 드는 MRP

사진 설명을 입력하세요.
아이가 잠이 드는 MP에 빨간색으로 보상 값이 추가된 것
MRP(Markov Process)

사진 설명을 입력하세요.
- 상태의 집합 S
- 마르코프 프로세스의 S와 같고, 상태의 집합
- 전이 확률 행렬 P
- 마르코프 프로세스의 P와 같고, 상태 s 에서 s'으로 갈 확률을 행렬 형태로 표현한 것
- 보상함수 R
- 어떤 상태 S에 도착했을 때 받게 되는 보상

사진 설명을 입력하세요.
- E(기댓값, 평균값)이 나오는 이유는 특정 상태에 도달했을때 받는 보상이 매번 조금씩 다를 수 있기에
- ex) 특정 상태에서 500원 동전을 던져서 앞면 : 500원, 뒷면 : 0원 => 기댓값 : 250원
- 감쇠인자 𝛾
- 0< 𝛾 <1 사이의 숫자
- 이는 강화 학습에서 미래에 얻을 보상에 비해 당장 얻는 보상이 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터
- 미래에 얻을 보상의 값에 𝛾가 여러 번 곱해지면서 그 값을 작게 만드는 역할함
- 감소된 보상의 합, 리턴
- 에피소드
- MRP에서는 MP와 다르게 상태가 바뀔때마다 해당하는 보상을 얻음
- 상태 S0에서 보상 RO를 받고 시작하여 종료 상태인 St에 도착할 때 보상 Rt를 받으며 끝남
- S0에서 St까지 가는 여정을 다음과 같이 표현

사진 설명을 입력하세요.
- 리턴(Gt)
- 리턴이란 t 시점부터 미래에 받을 감쇠된 보상의 합을 말합니다.
- 강화학습은 리턴을 최대화하도록 학습
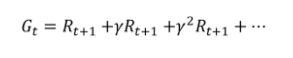
사진 설명을 입력하세요.
- 현재 타임 스템이 t 라면 그 이후에 발생하는 모든 보상의 값을 더해준다.
- 또 현재에서 멀어질 수록, 즉 더 미래에 발생할 보상일수록 γ가 여러 번 곱해진다.
- γ는 0에서 1 사이의 실수이기 때문에 여러 번 곱해질수록 그 값은 점점 0에 가까워 짐, 이때 γ 의 크기를 통해 미래에 얻게 될 보상에 비해 현재 얻는 보상에 가중치를 줄 수 있다
- 강화 학습은 보상이 아니라 리턴을 최대화 하도록 학습하는 것
- 다시말해, 보상의 합인 리턴이 바로 우리가 최대화하고 싶은 궁극의 목표
- 𝛾는 왜 필요할까?
- 𝛾=0 일때 미래의 보상은 모두 0 --> 매우 근시안적인 에이전트
- 𝛾=1 일때 매우 장기적인 시야를 갖고 움직이는 에이전트
- 1) 수학적 편리성
- 𝛾를 1보다 작게 해줌으로써 리턴 Gt가 무한의 값을 가지는 것을 방지
- 리턴이 무한한 값을 가질 수 없게 된 덕분에 이와 관련된 여러 이론들을 수학적으로 증명하기가 한결 수월해진다.
- 에피소드에서 얻는 각각의 보상의 최댓값이 정해져 있다면, Gt 는 유한하다.
- • γ 덕분에 MRP 를 무한한 스텝동안 진행하더라도 리턴 Gt 는 절대 무한한 값이 될 수 없다.
- 리턴이 무한이라면 어느 쪽이 더 좋을지 비교하기도 어렵고, 그 값을 정확하게 예측하기도 어려워짐
- • 감마가 1보다 작은 덕분에 이 모든 것이 가능해진다
- 2) 사람의 선호 반영
- 사람은 기본적으로 당장 벌어지는 눈앞의 보상을 더 선호
- 에이전트를 학습하는데 있어서 감마의 개념을 도입
- 3) 미래에 대한 불확실성 반영
- 현재와 미래 사이에는 다양한 확률적 요소
- 당장 느끼는 가치에 비해 미래에 느끼는 가치 변화 가능
- 미래의 가치에는 불확실성을 반영하고자 감쇠 인자 사용
- 그렇기 때문에 미래의 가치에는 불확실성을 반영하고자 감쇠해줌
- MRP에서 각 상태의 밸류 평가하기
- 어떤 상태를 평가할 때에는 그 시점으로부터 미래에 일어날 보상을 기준으로 평가
- MRP 자체가 확률적인 요소에 의해 다음 샅애가 정해지므로 리턴 역시 매번 변화
- 이것이 바로 리턴
- 하지만 리턴이라는 값은 매번 바뀐다는 문제가 있다.
- 왜냐하면 MRP 자체가 확률적인 요소에 의해 다음 상태가 정해지기 때문에 같은 s2 에서 출발해도 아이가 잠들 때까지 각기 다른 상태를 방문하며 그때마다 얻는 리턴의 값은 달라지기 때문
- 이런 이유 때문에 리턴의 기댓값을 사용하는 것이다.
- 에피소드의 샘플링
- 하나의 에피소드 안에서 경유하는 상태들은 매번 다름
- 매번 에피소드가 어떻게 샘플링 되느냐에 따라서 리턴 달라짐
- 예로 앞 뒷면의 확률의 반반인 동전 X의 확률 분포
- P(X - 앞면) = 0.5
- P(X = 뒷면) = 0.5
- 이를 샘플링 하면, 즉 동전을 던져보면 앞면 또는 뒷면이 나온다.
- 이 때 나온 하나의 면을 샘플이라 한다.
- 우리는 주어진 확률 분포에서 샘플링을 계속해서 할 수 있다.
- 정리하면 위와 같은 샘플링 기법을 통해 주어진 MRP 에서 여러 에피소드를 샘플링 해서 볼 수 있다는 것이다.
- 각 상태에 마치 동전 던지기와 같은 과정을 거쳐서 다음 상태가 정해짐
- 각 상태마다 다음 상태를 샘플링하며 진행하면 언젠가 종료 상태에 도달할 것이고 하나의 에피소드가 끝난다.
- 중요한 것은, 우리에게 전이 확률 행렬 P 가 주어져 있기 때문에 이런 샘플들을 원한다면 무한히 뽑아낼 수 있다는 점이다
- 상태 가치 함수
- 상태를 인풋으로 넣으면 그 상태의 밸류를 아웃풋으로 출력하는 함수
- 상태 s로부터 시작하여 얻는 리턴의 기댓값

사진 설명을 입력하세요.
- 아이가 잠드는 MRP 에서 상태 s0 에서 출발하여 발생할 수 있는 에피소드는 무한히 많고, 그때마다 리턴도 항상 다르다.
- 에피소드 4개를 샘플링 및 리턴 계산

사진 설명을 입력하세요.
- 마르코프 결정 프로세스(MDP)
- 앞 소개된 MP와 MRP에서 상태 변화는 자동으로 이루어짐
- 순차적 의사 결정에서 의사결정이 핵심이다.
- MDP의 정의
- MRP에 에이전트가 더해진 것
- 에이전트는 각 상황마다 액션(행동) 취함
- 해당 액션에 의해 상태가 변하고 그에 따른 보상

사진 설명을 입력하세요.
- 상태의 집합 S
- MP와 MRP에서의 S와 동일 ( 가능한 상태의 집합 )
- 액션의 집합 A
- 에이전트가 취할 수 있는 액션들
- 화성의 흙을 채집하는 탐사 로봇 - A=(앞으로 이동, 뒤로 이동, 흙 채집)
- 에이전트는 스텝마다 액션 중 하나를 취하며 그대따라 상태 변화
- 전이 확률 행렬 P
- 현재 상태 S이며 에이전트가 액션 a를 선택했을 때 다음 상태가 s’이 될 확률
- 같은 상태 s에서 같은 액션 a를 선택해도 매번 다른 상태에 도착할 수 있음

사진 설명을 입력하세요.
- 보상함수 R
- 현재 상태 s이며 에이전트가 액션 a를 선택했을때 받는 보상의 기댓값

사진 설명을 입력하세요.
- 감쇠인자 𝛾
- MRP에서의 𝛾과 정확하게 동일
- 아이 재우기 MDP

사진 설명을 입력하세요.
- 아이가 잠드는 상황에서의 어머니라는 에이전트가 개입되어 시작
- 상태 S일때 액션 a를 하게되면 확률적으로 다음 상태가 결정됨
- A = { a0 : “자장가를 불러줌” , a1 : “ 같이 놀아줌”)
- 상태 S2에서의 전이 확률 수식
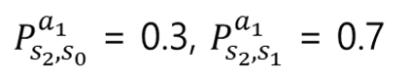
사진 설명을 입력하세요.
- 아이 재우기 MDP에서 보상의 합을 최대화 하기 위해서는 어머니라는 에이전트는 a0만을 선택하면 최적이라는것을 어렵지 않게 찾을 수 있다.
- MDP가 간단한 경우 최적의 전략을 찾기가 쉬워짐 , 반면 실제 세계의 MDP는 상태의 개수 및 액션의 개수가 훨씬 많기에 최적 행동을 찾는 것이 쉽지만은 않음
- 따라서 상황속에서 좋은 전략(=정책) 을 찾는 것이 우리의 목적이다.
- 정책 함수와 2가지 가치 함수
- 정책함수
- 각 상태에서 어떤 액션을 선택할지 정해주는 함수
- 𝜋를 사용해서 표기

사진 설명을 입력하세요.
- 확률을 이용한 정의는, 상태 s 에서 액션 a 를 선택할 확률로 해석
- 상태 가치 함수
- MDP 에서는 에이전트의 정책 함수에 따라서 얻는 리턴이 달라진다.
- 가치함수는 정책 함수에 의존적이다.

사진 설명을 입력하세요.
- s부터 끝까지 𝜋를 따라서 움직일 때 얻는 리턴의 기댓값
- 가치함수는 𝜋에 의존적
- 액션 가치 함수
- 액션 가치 함수는 q(s, a)로 표현합니다
- 상태에 따라 액션의 결과가 달라지기 때문에 상태와 액션이 동시에 인풋으로 들어가야 합니다.

사진 설명을 입력하세요.
- s 에서 a 를 선택하고, 그 이후에는 π 를 따라서 움직일 때 얻는 리턴의 기댓값
- 일단 s 에서 a 를 선택하고 나면 이후의 상태를 진행하기 위해 계속해서 누군가가 액션을 선택해야 하는데, 그 역할은 정책 함수 π 에게 맡긴다.
- 따라서 v(s) 와 q(s, a) 는 "s 에서 어떤 액션을 선택하는가" 하는 부분에만 차이
- Prediction과 Control
- Prediction
- π 가 주어졌을 때 각 상태의 밸류를 평가하는 문제
- Control
- 최적 정책 𝜋*를 찾는 문제
- 최적의 정책이란 이 세상에 존재하는 모든 π 중에 가장 기대 리턴이 큰 π 를 뜻함

사진 설명을 입력하세요.
- 최적 𝜋를 따를 때의 가치 함수를 최적 가치 함수라고 하며 v라고 표기함
- 최적 정책 𝜋* 와 최적 가치 함수 v* 를 찾았다면 이 MDP 는 풀렸다 라고 할 수 있음
728x90
'ML' 카테고리의 다른 글
| BDA_딥러닝의 이해반_0323_복습코드 (0) | 2025.03.28 |
|---|---|
| BDA_딥러닝의 이해반_250323 (0) | 2025.03.25 |
| 로지스틱 회귀 모델 (1) | 2024.07.04 |
| 비지도 학습 (0) | 2024.07.04 |
| 머신러닝 알고리즘 정리 (0) | 2024.07.04 |


