로지스틱 회귀 모델
- 로지스틱 회귀 모델을 이해하기 위해 경사 하강법과 컨벡스 함수 개념을 먼저 알아보자
경사하강법
- 주어진 비용 함수의 지역 최솟값이나 전역 최솟값을 구하는 것은 수학적 최적화 과정 중 하나인데, 경사 하강법은 이 과정을 수행하는 방법의 하나이다.
- 넚은 의미에서 경사하강법은 경사 혹은 그래이디언트의 역방향으로 입력값을 차례대로 이동하며 최소의 목푯값을 달성하는 모든 방법을 의미.
- 경사하강법 종류로는 최대하강법, 뉴턴법, BFGS 등 여러 알고리즘이 있다.
최대하강법
이중 가장 간단한 최대하강법임으로 이를 알아보면
- 이터레이션마다 해당 점의 그레이디언트를 구하고 그 역방향으로 그레이디언트의 상수 배만큼 좌표를 이동하며 지역 최솟값을 찾는 최적화 알고리즘
구현하기
- 함수 f(x)=x^2 을 최대하강법으로 구현
- 함수를 미분하여 f(x)=2x가 0이 되는 지점인 x-0이 해라는 것을 알 수 있고, 주어진 각각의 x에 대하여 f(x)값은 계산할 수 있지만 함수 형태가 매우 복잡하여 최솟값을 직접 유도할 수 없는 복잡한 경우 이 알고리즘을 적용하면 좋다는 것을 염두해 두고 구현을 진행
| import numpy as np import matplotlib.pyplot as plt %matplotlib inline x0, Delta, Tolerance = 2, 0.4, 0.005 |
- 초기점 x0 은 스텝 사이즈 Delta, 허용 오차 Tolerance 값을 정의
- Tolerance 는 허용오차 값을 정의한 것으로 정지 조건에 필요한 값 ( 이터레이션 중 파라미터 업데이트의 크기가 Tolerance 보다 작으면 학습을 중단시킴
- 이번 예시에서는 함수 구조를 통해 0에 가까워질수록 해에 가까워진다는 것을 알지만, 일반적으로는 최적화할 함수가 매우 복잡한 형태이므로 이터레이션을 진행해도 최솟값에 도달하는지 알 수 없다.
- 다만 이터레이션을 반복해도 점의 이동이 크지 않으면 이 근방이 최솟값일 것으로 판단하고 멈추는 것이다.
| def grad(x): return 2 * x |
- 그레이디언트를 계산하여 값을 반환하는 함수를 정의
- 함수화 하지않고 직접 미분한 형태를 바로 업데이트 식에 대입해도 되지만, 함수 형태가 복잡한 상황을 가정하면 그레이디언트의 함수식 정의는 딥러닝과 같이 체인 룰이 수많은 횟수로 중첩되어 적용되었을 때 매우 유용하게 쓸 수 있다.
| xs = [] x_prev = x0 for cnt in range(0, 100): cnt += 1 xs.append(x_prev) x_curr = x_prev - 2 * Delta * grad(x_prev) diff = np.abs(x_curr - x_prev) if diff <= Tolerance: break x_prev = x_curr print("이터레이션 횟수:", cnt) print("x_curr의 값:", x_curr) |
이터레이션 횟수: 14 x_curr의 값: 0.0015672832819200039
- 이터레이션별 상황을 추적하고 이터레이션을 수행하는 코드를 구현
- 학습 히스토리를 저장하고자 리스트 xs를 정의하고 이터레이션별 x값을 저장
출력을 보면 이 알고리즘은 14번의 이터레이션 후 근사하게 되고 약 0.001567이라는 답을 찾아내었다는것을 확인
실제 해는 0에 아주 가깝다는 것이다.
| plt.plot([i for i in range(cnt)], [0] * cnt, 'k', label='Optimum Parameter') plt.plot([i for i in range(cnt)], xs, 'r', label='Steepest Decsent') plt.legend() |
- 누적한 히스토리를 확인해보면 아래와 같다.
- 결과 그래츠는 이터레이션 횟수에 따른 점의 이동을 나타낸다.

- 추정 값이 해 위아래로 변하여 0에 가까워지는 것을 확인
- 스텝사이즈를 작게 설정하면 단방향으로 0으로 수렴하는 결과를 얻을수도 있다.
- 스텝사이즈 선택이 매우 중요한데, 스텝사이즈를 너무 작게 잡으면 이터레이션마다 변동폭이 너무 적어 수렴속도가 느려지고, 스텝사이즈를 너무 크게 설정하면 앞의 예와 같이 진동이 발생할 수 있다. 따라서 마찬가지로 수렴 속도가 느려질 수 있다.
- 스텝사이즈 선택 문제에도 최대하강법은 많이 사용하는 기법의 하나로, 최대하강법은 구조가 매우 간단하고 1계 도함수만 알면 충분히 구현할 수 있다.
많은 알고리즘은 최대하강법이 변형된 형태라고 볼 수 있다.
- 뉴턴법은 최대하강법에서의 스텝사이즈를 상수가 아나라 2계도함수의 역수인 1/f``(x)로 택하는 기법으로 좋은 스텝사이즈값을 이터레이션마다 사용자에게 지정해주기 위한 것으로 생각하면 좋다.
컨벡스 함수
- 함수 f가 컨벡스 함수라면 지역 최솟값이 전역 최솟값이 되는 매우 좋은 성질이 있다.
- 이때 전역 최솟값을 찾는 과정을 컨벡스 최적화라 하며, 유일한 해가 도출된다.
- ML의 경우 비용 함수를 최소화하는 과정을 거치게 되는데, 이때 비용 함수가 컨벡스 함수인지가 중요한 것이다.
- convex 함수란 임의의 두 점 x1, x2와 [0,1] 사이의 값 t에 대해 다음 부등식이 항상 성립하는 함수 f를 가리킨다.

- 용어
- Convex function: 볼록 함수
--> 아래로 볼록한 그래프의 개형을 가지는 함수를 뜻함.
- 정의 해석
- 두 점을 양 끝점으로 하는 선분의 벡터 방정식
정의에 나타난 부등식의 좌변을 보면 다음과 같은 형태를 찾아볼 수 있다.
이는 t의 값에 따라 정해지는 점 x1과 점 x2를 잇는 선분 위의 임의의 점을 나타낸다. 이러한 부분을 염두하고 그래프를 살펴보면 정의를 쉽게 이해할 수 있다.

즉, 함수 f가 Convex 라는 것은 f가 정의된 영역에서 임의의 두 점을 잡았을 때, 그 지점들에서의 함숫값을 이은 선분은 항상 실제 f의 그래프보다 항상 위에 있거나 같다는 것이다. 이는 아래로 볼록한 함수라는 것을 의미한다.
로지스틱 회귀 모델
- 로지스틱 회귀는 분류 문제를 해결하는 가장 기본적인 머신러닝 모델의 하나
- 문헌에 따라 로짓회귀, MaxEnt분류, 로그-선형 분류기 등으로 부르기도한다.
- 목표 클래스의 발생 확률을 로지스틱 함수로 모델링한다.
로지스틱 회귀 모델의 기본 이론
- 로지스틱 회귀 모델은 주어진 이진 목푯값 y의 클래스 레이블 값이 1이 나올 확률 p(y)와 피처 벡터 x사이의 관계를 모델링하는 기법
- 각각의 샘플 i(1≤i<n) 에 대하여 목푯값 yi가 다음과 같이 독립으로 생성된다.
로지스틱 회귀 모델 생성 과정
(1) 피처 벡터 Xi가 외뷔에서 결정 된다.
(2) yi는Xi와 w에 조건부로 정해지며 yi가 1이 될 확률이 p(yi|xi, w)로, 0이 될 확률이 1-p(yi|xi, w)로 주어지는 베루누이 분포를 따른다. 여기서 w는 추정하고자 하는 값이지만, 상수로 이미 주어져 있다고 가정한다.
(3) p(yi|xi, w) 에 따라 yi가 결정된다.
단변수 로지스틱 회귀 모델 최적화하기
- 단변수 로지스틱 회귀 모델은 주어진 독립 변수 X와 종속 변수 Y 사이의 관계를 설명하기 위해 사용된다. 종속 변수 Y는 이진(binary) 값(예: 0 또는 1)을 가지며, 로지스틱 회귀는 이러한 이진 결과를 예측한다.
뉴턴법을 이용하여 다중 로지스틱 회귀 모델 최적화하기


- 뉴턴법을 이용한 이미레이션은 그 폭이 너무 커 발산할 수 있으므로 실질적인 추정을 위해 학습률을 감쇄하는 파라미터 v(0<v<1)를 도입하는 수정 뉴턴법을 많이 사용한다. (데이터 형태에 따라 적절한 v값은 달라질 수 있지만 도메인 지식이 없다면 0.1 전후의 값을 선택하는 것이 좋다.)
로지스틱 회귀 모델 구현하기
sklearn 에서 제공하는 분류 데이터셋 중 데이터 규모가 비교적 큰 유방암 데이터셋을 이용하고, 맨 앞의 세 피처만 사용하여 모델링을 수행하였다.
| import numpy as np from sklearn.datasets import load_breast_cancer from sklearn.model_selection import train_test_split X, y = load_breast_cancer(return_X_y=True, as_frame = False) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1234) X_train, X_test = X_train[:, :3], X_test[:, :3] y_train, y_test = y_train.reshape(-1, 1), y_test.reshape(-1, 1) |
학습 데이터셋의 각 피처가 평균 0과 분산 1이 되도록 표준 스케일링을 수행, 이후 같은 평균과 표준편차를 똑같이 데이터셋에도 적용. 추가로 학습 데이터셋과 테스트 데이터셋에 각각 절편을 추가
| train_mean, train_std = X_train.mean(axis=0), X_train.std(axis=0) X_train, X_test = (X_train - train_mean) / train_std, (X_test - train_mean) / train_std n, n_test = X_train.shape[0], X_test.shape[0] X_train, X_test = np.append(np.ones((n, 1)), X_train, axis=1), np.append(np.ones((n_test, 1)), X_test, axis=1) |
최대 이터레이션 횟수와 조기 종료 조건을 설정하고 최대 10000번 반복하고, 파라미터 업데이트 크기가 유클리드 거리 기준으로 0.0001 이하가 되면 종료하는것으로 설정
파라미터 초기화 (정규분포에서는 무작위 추출 등 다양한 방법이 있지만 여기서는 편의상 모든 계수가 1인 상태를 초깃값으로 설정)
| max_iter = 10000 Tolerance = 0.0001 beta_old = np.ones((4, 1)) |
이터레이션을 수행, 구현은 앞서 w행렬과 p벡터를 정의한 후 이를 식에 대입하는 과정으로 이루어짐
numpy 배열의 행렬곱에는 @를 사용하는게 특징.
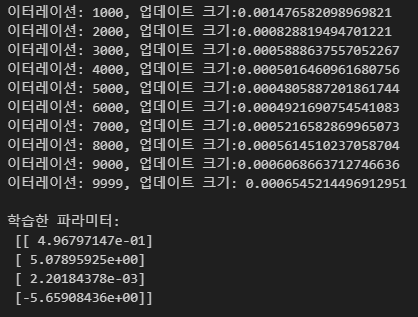
최대 이터레이션이 10000에 도달하면 종료하고 업데이트 크기가 5000번째 이터레이션을 기점으로 다시 증가하는것에 유의
이번 구현에서 파라미터 업데이트시 학습률 크기를 단순화 했지만, 이로 인해 이터레이션 5000회 이후에서는 상대적인 학습률의 크기가 필요 이상으로 커서 해가 발산하는 현상이 발생한 것으로 보인다. 실제로는 업데이트 크기가 계속 감소하다가 Tolerance 아래로 내려가 최대 이터레이션 도달 전에 종료하는 것이 매우 이상적이다.
이제 학습한 파라미터로 학습과 테스트 데이터셋에서 정확도를 계산해보았다.
학습 데이터셋 내 각 샘플에 대해 루프를 돌면서 옳은 예측치의 수를 세고, 이 수와 샘플 전체 수의 비율을 정확도로 했다.
| right = 0 for i in range(X_train.shape[0]): xb = np.exp((X_train[i].reshape(1, -1) @ beta_old)[0][0]) pi = xb / (1 + xb) if (pi >= 0.5 and y_train[i] == 1) or (pi < 0.5 and y_train[i] == 0): right += 1 print(f'학습 데이터셋 정확도:{right / X_train.shape[0] * 100: .2f}%') right = 0 for i in range(X_test.shape[0]): xb = np.exp((X_test[i].reshape(1, -1) @ beta_old)[0][0]) pi = xb / (1 + xb) if (pi >= 0.5 and y_test[i] == 1) or (pi < 0.5 and y_test[i] == 0): right += 1 print(f'테스트 데이터셋 정확도:{right / X_test.shape[0] * 100: .2f}%') |

수렴이 불안정함에도 비교적 높은 정확도를 얻었는데, 이는 데이터셋이 비교적 간단하고 로지스틱 회귀 모델의 비용 함수가 전역 최솟값을 가지므로 얻은 파라미터가 전역 최적값 근처에 있기 때문이라 생각된다.
- 여기서 모델을 개선해 더 높은 정확도를 얻으려면 비용 함수가 계속 줄도록 학습률을 조정하는 과정이 필요할 것이다.
'ML' 카테고리의 다른 글
| BDA_딥러닝의 이해반_0323_복습코드 (0) | 2025.03.28 |
|---|---|
| BDA_딥러닝의 이해반_250323 (0) | 2025.03.25 |
| 비지도 학습 (0) | 2024.07.04 |
| 머신러닝 알고리즘 정리 (0) | 2024.07.04 |
| 강화학습 1 (0) | 2024.05.29 |


